index

SQL(사실 “시퀄”이라고 말하는 게 아직도 더 편하긴 하다)을 덕질하기 시작한지 얼마 안됐는데 (아직도 JOIN이 헷갈리고 윈도우 함수나 CTE는 찍먹도 못해봄) 하면 할수록 쿼리를 날리는 여러가지 함수를 알고 그것을 써먹는 것을 살펴보는 것보다 ‘왜’ 그러한 함수를 써야하는가란 질문과 더불어 관계형 데이터베이스 자체가 어떻게 구성되어있는지가 궁금해졌다. 이 글은 그러한 내 개인적인 궁금증들을 해결하기 위해 남긴 기록들이다. 기본적으로 이 포스트 및 이후에 작성될 관련 포스트는 이 책을 기준으로 작성되었고, 필요하다면 추가적으로 다른 책들을 참고해서 내용들을 추가했다.

1. 관계형 모델이란?

먼저 이 “관계형 모델”이란 단어부터 쪼개보자. 모델은 모형이라는 뜻이며, 간단하게 말하면 이는 어떠한 틀이라 할 수 있다. 이 모형을 어떤 방식으로 쓰느냐에 따라서 그 구체적인 모양새가 조금씩 달라질 수 있지만, 그 기본적인 틀은 변하지 않는다. 그리고 이 모형이라는 틀은 데이터라는 자료를 담을 수 있으며, 그 자료는 구성된 요소들에 따라서 다양한 형태를 취할 수 있다. 따라서 우리는 모델이란 것은 임의의 형태를 지닌 자료, 즉, 데이터를 담는 모형이자 곧 틀이라 볼 수 있다.

그렇다면 관계형은 무엇일까? 즉, 관계(Relation)란 무엇일까? 테이블 사이의 관계라고 얘기할 수도 있지만, 이는 정확하지 않은 표현이다. 단도직입적으로 말한다면 SQL의 관점에서는 관계란 곧 테이블이다. 즉, 테이블은 관계의 집합이다. 좀 더 깊게 들어가보자. 우선 우리는 관계를 다음과 같이 얘기하고자 한다.

관계
- 제목(Heading)
  - 이름과 자료형으로 되어 있는 속성(Attribute) n개가 모인 집합 (이 때, n은 0개 이상의 정수)
- 본체(Body)
  - 속성 값의 집합인 행의 모임, 즉, 튜플의 집합

이 때 튜플의 집합, 즉, 튜플에 있는 값들은 그 이름과 자료형이 제목에서 지정한 것과 서로 일치해야 한다. 정리하면 관계란 튜플의 집합이고, 여기서 튜플은 모두 같은 n개의 속성값의 집합이며 그 구성이 서로 같은 것이라 할 수 있다. 그리고 우리는 이러한 관계들의 집합을 테이블이라 부른다.

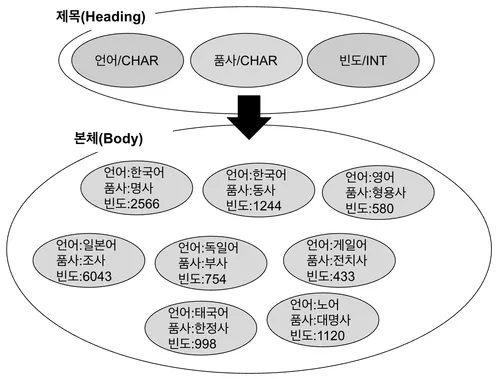
< Fig 1. >은 관계의 예시를 보여준다. 제목에는 각각 언어, 품사, 빈도라는 이름이 있고 이에 대응하는 자료형과 함께 속성으로서 총 3개의 원소가 모인 집합임을 알 수 있다. 본체는 이 제목의 각 속성에 대응되는 값들이 튜플로서 표현되어있는데, 이는 행으로서 표현될 수 있는 집합임을 의미한다.

따라서 관계형 모델이란 제목과 본체라는 서로 동일한 n개의 속성값을 지닌 튜플의 집합을 포함하고 있는 모형이 라고 얘기할 수 있다. 나아가 관계형 모델에서 튜플과 속성은 아래 표처럼 각각 SQL에서 행(row)와 열(column)에 대응하는 것임을 알 수 있다. 결국 관계형 모델은 관계라는 테이블을 하나의 뭉탱이로서 표현해내는 데이터베이스라 할 수 있다.

관계형 모델	SQL
관계	테이블
튜플	행(row)
속성	열(column)

2. 도메인(Domains), 속성(Attributes), 튜플(Tuples), 관계

사실 위 얘기는 다소 느슨하게 들리는 것 같다. 더 형식적으로 관계형 모델을 정의해보자. 먼저 우리는 도메인(Domain)을 다음과 같이 정의한다.

도메인(Domain) $D$ 란 원자값(atomic values)의 집합이다.

여기서 원자(atomic)란 도메인에 속한 각각의 값이 더 이상 쪼개어질 수 없음을 애기한다. 예컨대 위 < Fig 1. >에서 ‘언어’는 문자형으로 표현되는 자연어 집합으로 이루어진 도메인이고, ‘품사’ 또한 문자형으로 표현되는 품사 집합의 도메인이며, ‘빈도’는 정수형으로 표현되는 품사의 빈도수 집합의 도메인이다. 그리고 각 도메인에 속한 값들(여기선 한국어, 영어, 명사, 동사 등등)은 더 이상 쪼개어질 수가 없다. 따라서 도메인이란 그 이름과 자료형과 그 포맷이 주어진다라고 볼 수 있다.

관계 스키마(relation schema)란, 관계 이름 $R$ 과 속성(attributes) 리스트 $A_1, A_2, ... , A_n$ 로 이루어진 것이다. 여기서 각각의 속성(attribute) $A_i$ 가 어떤 관계 스키마 $R$ 내 도메인 $D$ 에 주어진 이름, 즉, 열(column)이라 할 때, $D$ 는 $A_i$ 의 도메인이라 부르며 dom( $A_i$ )와 같이 표현한다. 이 때, $R$ 은 이러한 관계의 이름이라 한다. 나아가 관계의 차수(degree (or arity))를 정의하는데, 이는 관계 스키마에서 속성의 갯수를 의미한다. 즉, 열의 갯수다. 예컨대 어떤 심리언어학 실험을 참여하는 실험참여자 관련 정보를 총 4개의 차수, 즉, 4개의 속성(=열) 형태로 담고 있는 관계는 다음과 같이 표현할 수 있다.

실험참여자(이름, 성별, 나이, 제2외국어)

각 속성의 자료형을 추가로 표기하고 싶다면 아래와 같이도 표현할 수 있다.

실험참여자(이름: string, 성별: string, 나이: integer, 제2외국어: string)

여기서 ‘실험참여자’는 관계의 이름이자 곧 4개의 속성을 갖고 있다. 그리고 각각의 속성에 대한 도메인은 다음과 같이 표현할 수 있다.

dom(이름) = 이름, dom(성별) = 성별, dom(제2외국어) = 한국어가 아닌 자연어.

앞서 정의한 관계 스키마 $R(A_1, A_2, ..., A_n)$ 에서 관계(또는 관계 상태(relation state))는 $n$ -튜플의 집합이며 이는 $r = <t_1, t_2, .., t_m>$ 또는 $r(R)$ 로 표현한다. 각 $n$ -튜플 $t$ 는 $n$ 개의 값 $t = <v_1, v_2, .. , v_n>$ 로 이루어진 순서가 있는 리스트다. 이 때, $v_i$ 는 $dom$ ( $A_i$ )의 원소이거나 혹은 NULL 값이며 $i$ 의 범위는 $1 \leqq i \leqq n$ 이다. 튜플 $t$ 의 $i$ 번째 값은 속성 $A_i$ 에 대응하며 $t[A_i]$ 또는 $t.A_i$ 로 표현한다.

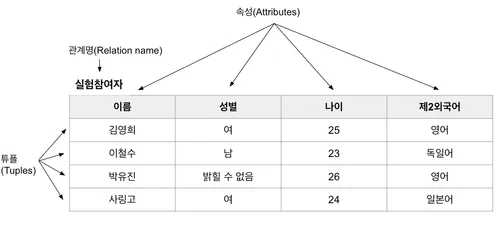
table_example — < **Fig 2**. 실험참여자 관계의 속성과 튜플 >

위 < Fig 2. >은 앞서 말했던 실험참여자 관계, 즉, 테이블을 보여준다. 이름, 성별, 나이, 제2외국어는 속성(=열)이며, 이에 대응대는 각 값의 나열을 튜플(=행)으로서 표현되는 것을 알 수 있다. 어떻게 coding 하느냐에 다를 수도 있겠지만, ‘밝힐 수 없음’은 NULL로서 대신 표기할 수도 있다.

2.1. 좀 더 엄밀하게 정의하기

위 정의들도 충분하지만, 사실 난 만족하지 않는다. 그래서 덕질을 더 할 거다. 좀 더 엄밀하게 다시 정의해보자. 사실 관계 $r(R)$ 은 도메인 $dom(A_1)$ , $dom(A_2)$ , … , $dom(A_n)$ 에 $n$ 차수(degree)로 이루어진 수리적 관계다. 그리고 이는 다른 말로 하자면 아래 $R$ 을 정의하는 도메인들에 대한 데카르트 곱(Cartesian Product)의 부분집합이다.

$r(R) \subseteq (dom(A_1) \times dom(A_2) \times ... \times dom(A_n))$

데카르트 곱은 모든 가능한 값의 조합을 반환해주므로 우리는 이를 집합의 크기(cardinality) 개념을 이용해 주어진 도메인 $D$ 내 있는 모든 값들의 갯수, 즉, 모든 튜플의 갯수를 아래와 같이 표현할 수 있다. 이 때 도메인은 유한하다고 가정한다.

이는 임의의 관계 $r(R)$ 에서 존재하는 모든 튜플들의 가능 조합을 표상하는 것이며, 이 때 특정 시점에 해당되는 관계를 현재 관계 상태(current relation state)라 한다. 해당 상태는 실제 세계에 있는 특정 상태에서만 가능한 튜플의 조합을 표상한다. 즉, < Fig 2. > 또한 어떤 현재 관계 상태인 것이다.

2.1.1. 튜플 내 값은 정말로 순서가 있는 걸까?

위에서 언급했듯 n-튜플 $t = < v_1, v_2, ..., v_n >$ 에서 $v$ 들은 순서가 있는 리스트라 하였다. 그러나 관계라는 것은 튜플로 이루어진 집합으로서 정의된다는 점을 생각해봤을 때, 실제로 튜플의 집합, 즉, 행의 경우 서로 순서가 없는 것이 자명하다. 특히나 논리/추상적인 차원에서는 속성과 그 값(=튜플)이 서로 대응만 한다면 더욱 더 그러하다. 따라서 우리는 관계를 다음과 같이 재정의 할 수 있다

관계 스키마 $R = \{ A_1, A_2, ..., A_n \}$ 은 속성의 집합이고 (순서가 있는 리스트로 이루어진 속성이 아님!), 관계 상태 $r(R)$ 은 사상들로 이루어진 유한 집합(a finite set of mappings) $r = \{ t_1, t_2, ..., t_m \}$ 으로 이루어져 있다고 하자. 이 때, 각 튜플 $t_i$ 는 $R$ 에서 $D$ 가는 하나의 사상(mapping)이고 여기서 $D$ 는 속성 도메인의 합집합이다. 즉, $D = dom(A_1) \cup dom(A_2) \cup ... \cup dom(A_n)$ 이다. 따라서 이 정의에서 $t[A_i]$ 는 $r$ 내 각 사상 $t$ 가 $1 \leqq i \leqq n$ 에 따라 일어나는 $dom(A_i)$ 에 속해야한다.

이렇게 튜플을 하나의 사상으로 보게 된다면 얘기가 좀 더 쉬워질 수 있다. 즉, 튜플을 속성과 값으로 이루어진 쌍으로 이루어진 집합이란 것이다. 즉, $t = \{ <A_1, v_1>, <A_2, v_2>, ..., <A_i, v_i> \}$ 가 되는 셈이다. 이 때 각 쌍 $<A_i, v_i>$ 는 $dom(A_i)$ 에서 속성 $A_i$ 에서 그 값 $v_i$ 를 통해 나올 수 있는 사상의 반환값이다. 따라서 속성의 순서, 즉, 튜플 내 값의 순서는 이 정의에선 중요치 않다. 예컨대 아래 두 개의 튜플은 서로 동일한 것이다.

$t = <$ (이름: 김영희), (성별: 여), (나이: 25), (제2외국어: 영어) $>$

$t = <$ (성별: 여), (이름: 김영희), (제2외국어: 영어), (나이: 25) $>$

3. 관계의 연산

위에서 살펴봤다시피 관계형 모델은 기본적으로 집합론을 근간으로 삼고 있다. 그렇기에 관계형 모델을 이해하려면 집합에 대해서 정확히 알고 있는 것이 중요한데, 기본적으로 이 두 가지만큼은 꼭 알고있자.

어떤 원소가 집합에 포함되어 있는지 판정 가능해야 한다.
- 이는 다음과 같이 지시함수/특성함수를 이용해 간단히 표현할 수 있다.

\chi_A(x) = \begin{cases} 1 & \text{if } x \in A \\ 0 & \text{if } x \notin A \end{cases}

집합의 원소는 서로 중복되지 않으며, 각 원소는 그 자체로 유일하다.
- 예컨대, $\{1, 2, 3, 3\} = \{1, 2, 3\}$ 에서는 사실 3이 두 번 나온 건 그닥 중요하지 않으며 각 원소 그 자체가 유일하다. 요건 ZFC 공리계에서 아래 외연공리에 의해 나올 수 있는 거다.

(\forall x \in A, \; x \in B) \;\land\; (\forall x \in B, \; x \in A) \;\;\;\;\Leftrightarrow\;\;\;\; A = B

따라서 관계란 것은 결국 집합이다. 집합이니깐 당연히 연산이 가능할 것인데, 관계형 모델에서 그 연산은 쿼리(Query), 즉, 질의가 담당한다. 이를 통해 우리는 관계형 모델은 관계라는 단위로 다양한 연산을 쿼리를 통해 수행하는 데이터 모델로 생각해볼 수 있다. 그러나 이 관계라는 집합은 우리가 흔히들 생각하는 수학에서의 집합에서 사용하는 연산과는 살짝 다르다. 그 이유는 관계 내의 튜플이 모두 같은 구조를 갖기 때문이다. 따라서 관계형 모델에서는 기존 집합 연산과 동일한 것들도 볼 수 있지만, 그 특성에 의해서 관계형 모델에서 이루어질 수 있는 특유의 연산이 더 있다. 기본 연산부터 순서대로 살펴보자.

제한(Restrict)

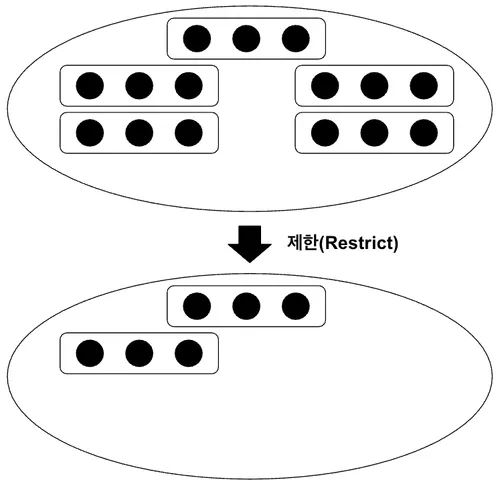
제한은 어떤 관계 중에 특정 조건에 부합하는 튜플을 포함한 관계를 반환한다. 즉, 부분집합이다. 이는 본래의 관계 또는 공집합 또한 반환할 수 있다는 뜻이다.

투사(Projection)

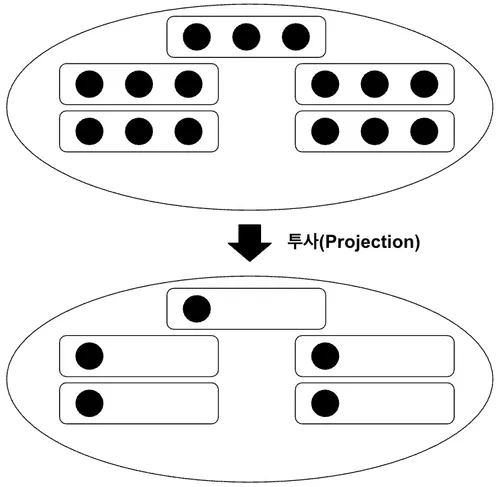
투사는 어떤 관계에서 특정 속성만 포함하는 관계를 따로 반환한다.

확장(Extension)

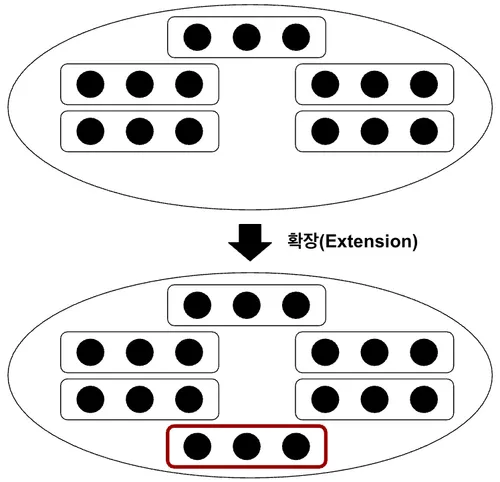
확장은 속성을 늘리는 연산으로, 이는 투사와는 반대의 기능을 한다. 대부분 새로운 속성값은 기존의 속성값을 이용해 반환된다.

속성명 변경(Rename)

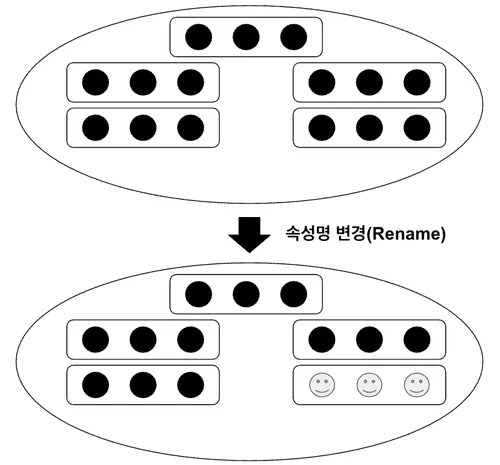
말 그대로 속성의 이름을 변경하는 계산이다. 위 < Fig 3.4. >에서는 단순 원에서 이모지 ”🙂” 혹은 미소로 변경된 것을 속성명 변경이라 할 수 있다. 이처럼 실제로 속성명 변경의 경우 주로 확장된 속성에 대한 명칭을 부여할 때 사용한다.

합집합(Union)

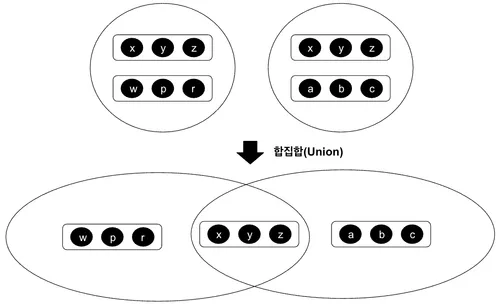
합집합은 예컨대 두 개의 관계가 각자 갖고 있는 튜플들을 하나로 합쳐 반환한다. 이 때, 서로 공통된 속성값이 있다면 중복값은 제거된 상태로 반환한다.

교집합(Intersection)

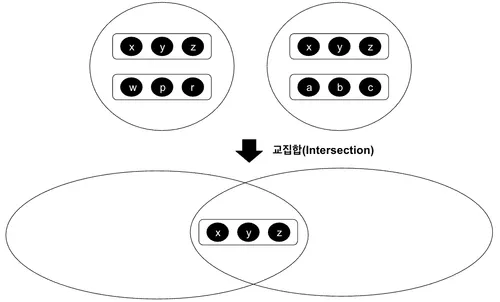
교집합 또한 두 개의 관계가 있을 때 각자 갖고 있는 튜플들을 반환하는 것이지만 서로 공통된 튜플만을 반환한다는 점에서 차이가 있다.

차집합(Difference)

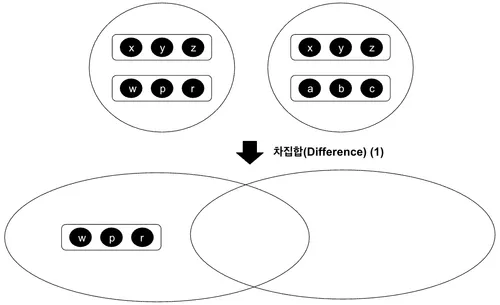
difference_1 — < **Fig 3.7**. 차집합 예시 (첫번째) >

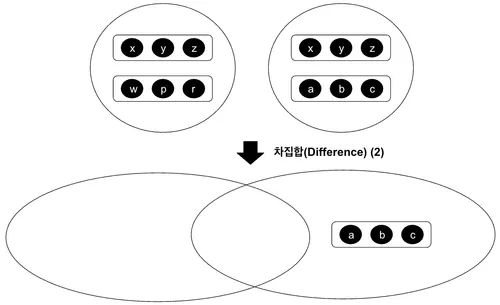
difference_2 — < **Fig 3.8**. 차집합 예시 (두번째) >

차집합은 두 개의 관계 중 한 쪽에만 포함되어 있는 튜플로 구성된 관계를 반환한다. 이 때 주의할 점이 있는데, 바로 < Fig 3.7. >, < Fig 3.8. >처럼 어느 관계를 기준으로 차집합 연산을 하느냐에 따라 결과가 달라질 수 있다는 점이다.

곱집합(Product)

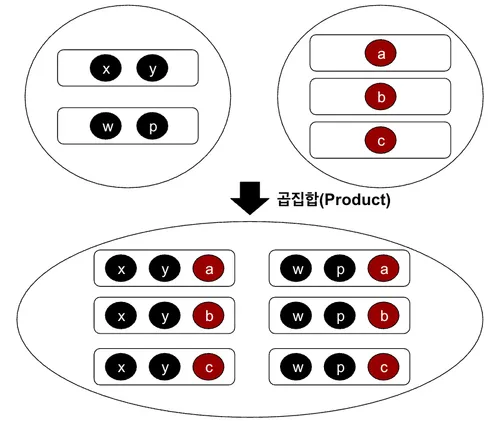
곱집합은 두 개의 관계에 있는 튜플을 각각 조합된 관계를 반환한다. < Fig 3.9. >를 기준으로 본다면 이는 $\{x, y\} \times \{a, b, c\}$ 와 $\{w, p\} \times \{a, b, c\}$ 이 반환한 값과 동일하다. 이렇게 반환된 관계가 있을 때 그 제목은 기존 관계의 제목이 가진 속성을 모두 포함한다.

결합(Join)

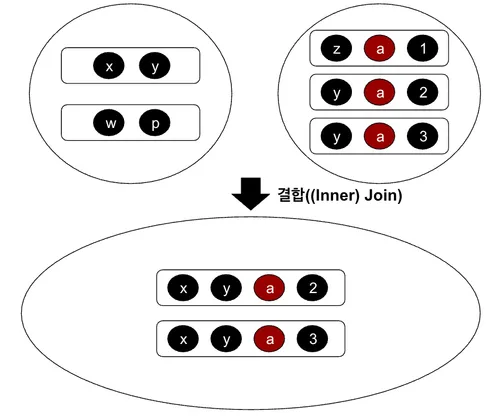
결합은 공통된 속성을 가진 관계에서 서로 동일한 속성값을 가진 튜플끼리 조합한 관계를 반환한다. 즉, 서로 일치하지 않는 값을 지닌 튜플을 제외한 채 반환하는 것이다. 이는 SQL에서 내부결합(Inner Join)과 동일하다.

지금까지 대표적인 관계 연산들을 살펴보았다. 주지했듯 분명 기존 수학의 집합의 연산과 사실상 동일한 것이 있는가 하면, 관계형 모델이 지닌 특성으로 인한 특수한 연산 또한 존재한다. 요점은 이렇나 연산을 이용해 관계로부터 필요한 정보를 추출할 수 있다는 것이고, 이게 바로 쿼리의 본질이라는 것이다. 결국 이러한 연산들을 잘 숙지한 상태로 SQL 쿼리를 작성함으로써 현재 사용하고 있는 RDB의 성능을 최대한 끌어내야하는 것이다.

폐쇄(Closure) 성질

관계형 모델의 중요한 특징 중 하나는 바로 관계를 사용한 연산 결과가 바로 (또 다른) 관계라는 것이다. 이는 자료형이 integer인 숫자 두 개를 갖고 연산한 값이 다시 integer인 값을 반환하고 그 결과를 갖고 다른 동일한 자료형의 값을 또 연산하는 것과 똑같다. 이처럼 연산의 입력과 출력이 같은 자료형을 가진 성질을 폐쇄(Closure)라고 하는데, 바로 이러한 성질 때문에 관계 연산은 마치 꼬리에 꼬리를 무는 것처럼 복잡한 연산을 표현할 수 있게끔 해준다. 그리고 이는 관계형 모델의 주요 특징 중 하나다.

관계형 모델의 자료형

자료형이 언급된 김에 관계형 모델의 자료형에 대해 간단히 얘기해보자. 사실 관계형 모델이 어떤 자료형을 사용할 지를 정하지는 않는다. 왜냐하면 이는 그저 모델, 즉, 모형이기 때문에 어떻게 사용할 수 있는지만 정해져 있을 뿐, 어떻게 사용해야한다란 제약은 모델을 사용하는 프로그램에 달려있다. 예컨대 C 언어에서 변수를 int나 float할지 여부는 결국 C 언어, 더 나아가서 이를 선언하는 프로그래머가 그 주체성을 갖고 있다.

어떻게 본다면 자료형은 유한집합이라 볼 수 있다. int형이라면 오직 그 변수들은 int형만 있는 것처럼 말이다. 이는 위에서 설명했던 도메인의 한 예시라 볼 수 있다.

3.1. SQL에서의 관계 연산

이번에는 SQL에서 사용되는 쿼리가 관계 연산에 어떻게 대응되는지 살펴보자.

SELECT

SELECT는 SQL에서 데이터를 조회하는데 사용되는 명령어다. 아래 SQL 쿼리를 살펴보자.

1
SELECT  t1.c1, t2.c3, ...   # 칼럼의 목록(=투사)   step 3
2
  FROM  t1, t2, ...         # 테이블 목록(=곱집합)  step 1
3
  WHERE t1.c4 = t2.c5, ...;  # 검색 조건(=제한)    step 2

관계 연산 관점에서 본다면 위 쿼리에서 테이블 목록을 읽는 과정인 FROM은 곱집합에 해당되고 (좀 더 직관적인 예시라면 FROM t1 INNER JOIN t2가 되겠다.), 검색 조건을 설정하는 WHERE은 제한에 해당되며, 마지막으로 칼럼의 목록을 출력해내는 SELECT은 투사라 할 수 있다. 그리고 이 연산 과정은 주석에도 표기되어있듯 FROM -> WHERE -> SELECT순으로 이루어진다. 이를 말로 풀어 쓰면 다음과 같다.

Step 1. 임의의 테이블 $t_1, t_2, ... t_n$ 을 읽어 이들에 대한 곱집합 연산 결과를 하나의 관계로 반환한다.

Step 2. 반환된 관계에 대해 제한 연산을 수행함으로써 그 부분집합을 얻어 특정 검색 조건을 만족시킨 것에 대한 관계를 반환한다.

Step 3. 반환된 관계에 대해 투사 연산을 수행함으로써 기존 검색 조건에 해당되는 특정 속성만 포함하는 관계를 반환한다.

보다시피 관계에서 시작해 관계를 반환하고 거기에 또 관계를 반환하는 방식이다. 여기서 한 가지 알아두어야할 점은 이러한 쿼리 수행 순서와 실제 RDB에서 수행되는 순서가 항상 동일하지는 않는다는 것이다. 대부분의 경우 RDB에서는 최적화 과정에 따라서 그 실행순서가 생략되거나 혹은 다르게 될 것이다. 예를 들어, 모든 칼럼을 출력한다기보다는 필요한 칼럼만 출력할 것이고 이 때 필요하게 될 칼럼들은 사실 WHERE 절의 조건에 따라서 최소화되므로 곱집합을 수행하는 경우는 없을 수가 있다. 중요한 것은 위 쿼리에서 일어나는 연산 순서는 어디까지나 관계형 모델에서 이루어지는 논리적 절차이라는 것이고, 실제 RDB에서는 최적화를 위해 달라질 수 있다는 점을 기억하는 것이다. 어찌됐든, SELECT는 논리 곱집합, 제한, 투사 이 세 가지 관계 연산을 함께 수행하는 작업이라 볼 수 있다.

참고로 확장 연산의 경우, 흔히들 사용하는 SELECT c1, c2, .. AS new_column에 해당되며 이 확장은 투사 직전에 수행된다.

INSERT

INSERT (INTO)는 기존 테이블에 새로운 행을 추가하는데 사용된다. 이는 어떻게 본다면 기존 테이블을 갱신 하는 것이라 할 수 있는데, 관계형 모델의 경우 릴레이션 그 자체가 어떤 반환된 값이기에 엄밀하게 본다면 갱신한다고 얘기하기엔 적합하지 않을 수도 있다. 다음 파이썬 코드를 생각해보자.

1
a = 1
2
a = a + 2
3
print(a) # 3

위 코드에서 a에 1이라는 값을 대입하고, 그 a를 a + 2로 변환하면 a는 3을 대입받은 상태가 된다. 이 때 갱신된 것은 값이 들어있는 곳, 즉, a라는 변수다. 마찬가지로 언급했듯 관계 또한 연산 결과로 인해 반환된 하나의 값이며 이는 갱신되지 않는다.

하지만 SQL에서는 테이블 내 값을 변경함으로써 갱신할 수 있다. 이렇게 되면 INSERT는 행을 추가함으로써 기존 테이블의 값인 관계가 바뀌는 것처럼 보인다. 이는 테이블이 값과 변수라는 역할을 둘 다 하기 때문인데, 관계형 모델에서 이렇게 관계를 저장하는 변수를 Relvar(Relation Variable) 혹은 관계 변수라고 한다. SQL에서는 이 테이블의 관계를 담당함과 동시에 Relvar의 역할도 갖고 있기에 갱신이 가능한 것이다.

이렇게 본다면 INSERT는 다음과 같이 생각할 수 있다. INSERT는 Relvar의 값, 즉, 관계를 기존 관계에 새롭게 행으로서 추가하고 바꾸는 작업이라 볼 수 있다. 그리고 Relvar을 R라 하고, 새로 삽입될 행에 대한 튜플을 T라 한다면 다음와 같이 표현할 수 있다.

$R := R \cup \{ T \}$

이는 사실상 합집합 연산을 진행하는 것과 동일하다. SQL문으로 치환하면 아래와 같다.

1
INSERT INTO t (c1, c2, c3) VALUES (1, 2, 3);

DELETE

기본적으로 DELETE문은 다음과 같이 SQL에서 시행된다.

1
DELETE FROM t WHERE c1 = 100;

관계형 모델의 입장에서 본다면, t라 전체 관계(=Relvar에 대입되는 값)라 할 때 여기서 c1 = 100이란 제한, 즉, 부분집합이 되어 그 차집합을 Relvar에 대입하는 것과 동일하다. 그리고 이는 다음과 같이 표현 가능하다.

$R := R - \{ T \}$

좀 더 직관적인 표현으로 쓴다면, Relvar을 WHERE 절의 조건에 만족하지 않는 튜플로 이루어진 관계로 바꾸는 거라고도 할 수 있다.

UPDATE

이어서 UPDATE (SET)문의 기본적인 예시를 살펴보자.

1
UPDATE t SET c1 = 1 WHERE c2 = 123

c2 = 123이라는 조건에 충족하는 테이블에서 c1 = 1로 갱신하라는 쿼리다. 관계형 모델 입장에서 본다면 위 쿼리는 다음과 같이 시행된다.

Step 1. 전체 관계에서 WHERE 절의 조건을 만족하는 튜플로 이루어진 관계의 차집합인 관계를 반환한다.

Step 2. 반환된 관계와 수정을 한 관계와의 합집합을 연산해 반환한다.

Step 3. 반환된 결과 관계를 Relvar에 대입한다.

그리고 위 과정은 다음과 같이 표현 가능하다.

$R := (R - \{ T_1 \}) \cup \{ T_2 \}$

4. SQL엔 있고 관계형 모델에는 없는 것

지금까지 SQL에서 이루어지는 연산(혹은 명령어)들이 관계형 모델의 입장에서 어떻게 논리적으로 이루어지는지 살펴보았다. 관계형 모델이 논리를 구성한다면, SQL은 그 논리를 실제 행동으로 치환해 구현되는 것으로 볼 수도 있다. 이는 다른 말로 하자면 관계형 모델에서 이루어지는 논리들을 잘 알고 있고, 이것이 SQL 수준에서는 어떻게 구현되고 차이를 보이는지 알고 있다면 좀 더 깊은 수준에서 쿼리를 짤 수 있게 된다는 거다.

우리는 지금까지 관계형 모델에는 있지만 SQL에는 없는 것(예: FROM 명령어가 수행될 때 관계형 모델에서는 곱집합으로 표현되지만 SQL에는 그렇지 않을 수도 있다는 점)을 살펴보았는데, 이번엔 반대로 SQL에는 있지만 관계형 모델에는 존재하지 않는 것을 살펴보자.

요소의 중복

관계는 서로 속성이 동일한 튜플의 집합이다. 이는 튜플이 중복될 수가 없다는 것을 의미하는데, SQL의 경우 테이블에서 같은 행(=튜플)이 있는 것을 허용한다. 물론 기본 키(Primary Key)가 있다면 유일성 제약에 의해 중복행을 허용하지 않겠지만, 그렇지 않다면 허용된다. 따라서 SQL에서의 테이블은 우리가 앞서 정의했던 관계에 대한 집합이라기보단, 중복집합(Multiset)이라 할 수 있다.

요소 사이의 순서

관계형 모델에서의 집합은 순서를 보장하지 않는다. 즉, 순서가 없다. 반면 SQL의 경우 ORDER BY와 같은 명령어를 통해 순서를 보장할 수 있다.

트랜잭션(Transaction)

SQL에서 트랜잭션은 중요한 요소이지만, 관계형 모델 입장에선 따로 떨어진 독립적인 개념이다. 따라서 관계형 모델에는 트랜잭션은 포함되지 않는다.

5. 정리

지금까지 관계형 모델과 SQL의 차이를 살펴봤다. 물론 실제로 SQL을 사용하는 사람 입장에서는 관계형 모델이 어떻게 이루어지는 중요하지 않을 수도 있고, 사실 이 글을 적고 있는 나조차도 좀 TMI가 아닌가 싶지만(…) 그럼에도 관계형 모델이 결국 모든 RDB의 시작이고, 따라서 관계형 모델이 지닌 특성들을 실제 RDB에 적용할 수 있는지 여부를 구분지어 알아두는 건 중요하지 않을까 싶다.

참고문헌

오쿠노 미키야. (2016). 관계형 데이터베이스 실전 입문. (성창규, 역). 위키북스. (원본 출판 2015년)

Elmasri, R. & Naavathe, S. B. (2017). Fundamentals of Database Systems (7th Edition). Pearson.

Ramakrishnan, R. & Gehrke, J. (2003). Database Management Systems. McGraw Hill.

[DB] SQL과 관계형 모델